NEAT is a neural network structure developed by Stanley and Miikkulainen (2002). NEAT optimizes both the structure and weights of a neural network with a genetic algorithm (GA). The input and output of a NEAT neural network are identical to a typical feedforward neural network, as seen in previous chapters of this book.
A NEAT network starts out with only bias neurons, input neurons, and output neurons. Generally, none of the neurons have connections at the outset. Of course, a completely unconnected network is useless. NEAT makes no assumptions about whether certain input neurons are actually needed. An unneeded input is said to be statistically independent of the output. NEAT will often discover this independence by never evolving optimal genomes to connect to that statistically independent input neuron.
Another important difference between a NEAT network and an ordinary feedforward neural network is that other than the input and output layers, NEAT networks do not have clearly defined hidden layers. However, the hidden neurons do not organize themselves into clearly delineated layers. One similarity between NEAT and feedforward networks is that they both use a sigmoid activation function. Figure 1 shows an evolved NEAT network:
Figure 1: NEAT Network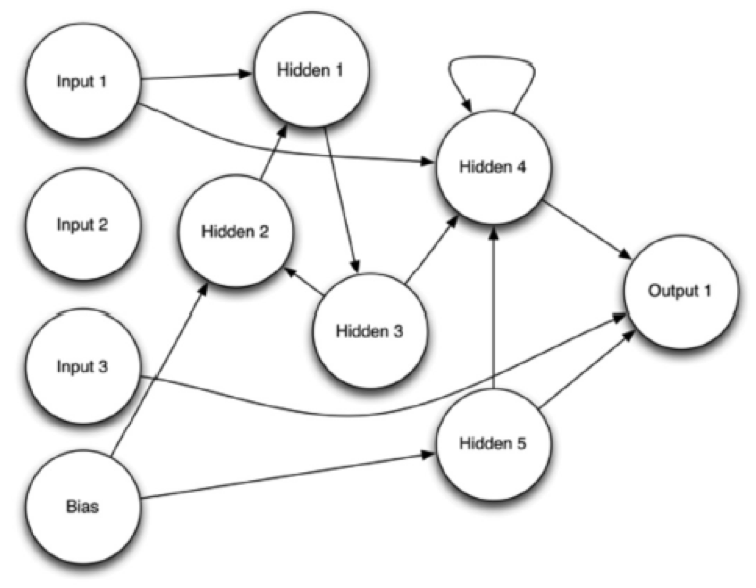
Input 2 in the above image never formed any connections because the evolutionary process determined that input 2 was unnecessary. A recurrent connection also exists between hidden 3 and hidden 2. Hidden 4 has a recurrent connection to itself. Overall, you will note that a NEAT network lacks a clear delineation of layers.
You can calculate a NEAT network in exactly the same way as you do for a regular weighted feedforward network. You can manage the recurrent connections by running the NEAT network multiple times. This works by having the recurrent connection input start at 0 and update them each type you cycle through the NEAT network. Additionally, you must define a hyper-parameter to specify the number of times to calculate the NEAT network. Figure 8.2 shows recurrent link calculation when a NEAT network is instructed to cycle three times to calculate recurrent connections:
Figure 2: Cycling to Calculate Recurrences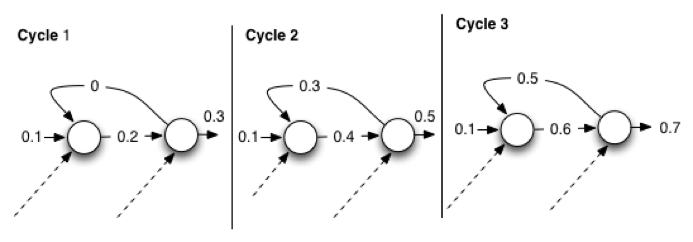
The above diagram shows the outputs from each neuron, over each connection, for three cycles. The dashed lines indicate the additional connections. For simplicity, the diagram doesn’t have the weights. The purpose of Figure 2 is to show that the recurrent output stays one cycle behind.
For the first cycle, the recurrent connection provided a 0 to the first neuron because neurons are calculated left to right. The first cycle has no value for the recurrent connection. For the second cycle, the recurrent connection now has the output 0.3, which the first cycle provided. Cycle 3 follows the same pattern, taking the 0.5 output from cycle 2 as the recurrent connection’s output. Since there would be other neurons in the calculation, we have contrived these values, which the dashed arrows show at the bottom. However, Figure 8.2 does illustrate that the recurrent connections are cycled through previous cycles.
NEAT uses a typical genetic algorithm that includes:
- Mutation – The program chooses one fit individual to create a new individual that has a random change from its parent.
- Crossover – The program chooses two fit individuals to create a new individual that has a random sampling of elements from both parents.
All genetic algorithms engage the mutation and crossover genetic operators with a population of individual solutions. Mutation and crossover choose with greater probability the solutions that receive higher scores from an objective function. We explore mutation and crossover for NEAT networks in the next two sections.
NEAT Mutation
NEAT mutation consists of several mutation operations that can be performed on the parent genome. We discuss these operations here:
- Add a neuron: By selecting a random link, we can add a neuron. A new neuron and two links replace this random link. The new neuron effectively splits the link. The program selects the weights of each of the two new links to provide nearly the same effective output as the link being replaced.
- Add a link: The program chooses a source and destination, or two random neurons. The new link will be between these two neurons. Bias neurons can never be a destination. Output neurons cannot be a source. There will never be more than two links in the same direction between the same two neurons.
- Remove a link: Links can be randomly selected for removal. If there are no remaining links interacting with them, you can remove the hidden neurons, which are neurons that are not input, output, or the single bias neuron.
- Perturb a weight: You can choose a random link. Then multiply its weight by a number from a normal random distribution with a gamma of 1 or lower. Smaller random numbers will usually cause a quicker convergence. A gamma value of 1 or lower will specify that a single standard deviation will sample a random number of 1 or lower.
You can increase the probability of the mutation so that the weight perturbation occurs more frequently, thereby allowing fit genomes to vary their weights and further adapt through their children. The structural mutations happen with much less frequency. You can adjust the exact frequency of each operation with most NEAT implementations.
NEAT Crossover
NEAT crossover is more complex than many genetic algorithms because the NEAT genome is an encoding of the neurons and connections that comprise an individual genome. Most genetic algorithms assume that the number of genes is consistent across all genomes in the population. In fact, child genomes in NEAT that result from both mutation and crossover may have a different number of genes than their parents. Managing this number discrepancy requires some ingenuity when you implement the NEAT crossover operation.
NEAT keeps a database of all the changes made to a genome through mutation. These changes are called innovations, and they exist in order to implement mutations. Each time an innovation is added, it is given an ID. These IDs will also be used to order the innovations. We will see that it is important to select the innovation with the lower ID when choosing between two innovations.
It is important to realize that the relationship between innovations and mutations is not one to one. It can take several innovations to achieve one mutation. The only two types of innovation are creating a neuron and a link between two neurons. One mutation might result from multiple innovations. Additionally, a mutation might not have any innovations. Only mutations that add to the structure of the network will generate innovations. The following list summarizes the innovations that the previously mentioned mutation types could potentially create.
- Add a neuron: One new neuron innovation and two new link innovations
- Add a link: One new link innovation
- Remove a link: No innovations
- Perturb a weight: No innovations
You also need to note that NEAT will not recreate innovation records if you have already attempted this type of innovation. Furthermore, innovations do not contain any weight information; innovations only contain structural information.
Crossover for two genomes occurs by considering the innovations, and this trait allows NEAT to ensure that all prerequisite innovations are also present. A naïve crossover, such as those that many genetic algorithms use, would potentially combine links with nonexistent neurons.