This example allows you to train a neural network using online backpropagation training. The training data used the XOR function, so the neural network should output the following:
When I1=0 and I2=0 then output 0 When I1=1 and I2=0 then output 1 When I1=0 and I2=1 then output 1 When I1=1 and I2=1 then output 0Because this is online training you can train any of the above four patterns individually, or you can train all 4 at once. Either way, the weights are adjusted after each pattern.
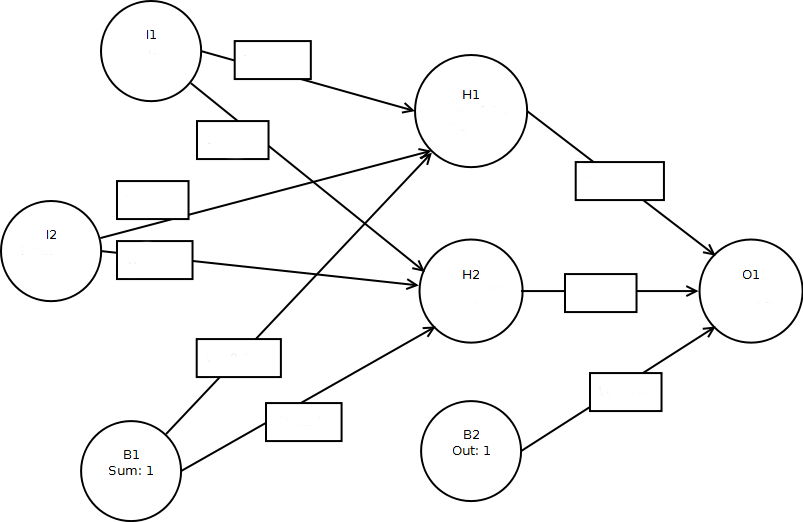
Training
Learning rate: , Momentum:
Mean Square Error(MSE):
- Input: [0,0], Desired Output: [0],
- Input: [1,0], Desired Output: [1],
- Input: [0,1], Desired Output: [1],
- Input: [1,1], Desired Output: [0],
Calculations
More Info
The following formulas are used in the above calculations.The sigmoid function is calculated with the following formula: $$S(t) = \frac{1}{1 + e^{-t}}.$$ The derivative of the sigmoid function: $$S'(x) = S(x) * ( 1.0 - S(x) )$$ Mean Square Error(MSE) is calculated with the following formula: $$ \operatorname{MSE}=\frac{\sum_{t=1}^n (\hat y_t - y)^2}{n}. $$ Output Layer Error is calculated with the following formula: $$ E = (a-i) $$ Node delta is calculated with the following formula: $$ \delta_i = \begin{cases}-E f'_i & \mbox{, output nodes}\\ f'_i \sum_k w_{ki}\delta_k & \mbox{, interier nodes}\\ \end{cases} $$ Gradient is calculated with the following formula: $$ \frac{ \partial E}{\partial w_{(ik)}} = \delta_k \cdot o_i $$
